Mécanique des fluides
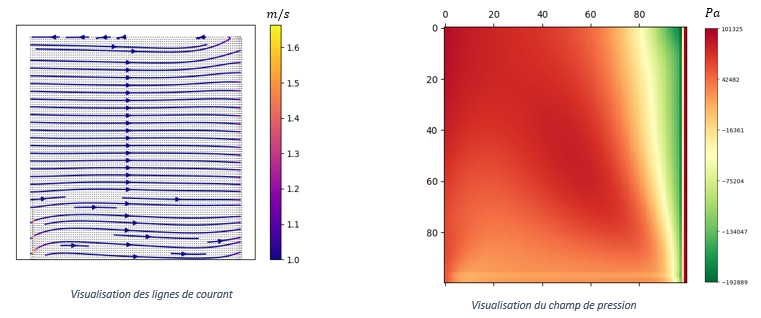
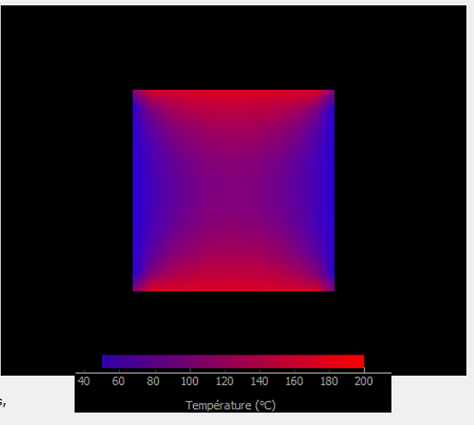
Ce groupe a travaillé sur les équations de Navier-Stokes afin de simuler l'écoulement d'un fluide dans un tuyau, associé à la veine d'essai de la soufflerie, et ainsi comparer les résultats obtenus avec celle-ci. Le programme étant très compliqué et très lourd, il n'a pas été possible de le transformer en exécutable. Le code a été réalisé en utilisant la méthode des différences finies qui permet de discrétiser des équations aux dérivées partielles comme celles de Navier-Stokes. Dans ce projet, le domaine d’étude est en 2 dimensions mais la transformation du code numérique pour un domaine 3D est possible. On associe alors la veine d’essai de la soufflerie à un domaine rectangulaire. La paroi verticale gauche est la paroi par laquelle le fluide entre dans le domaine d’étude, la paroi droite par celle où il sort. Les deux parois horizontales sont des murs que le fluide ne peut pas traverser.
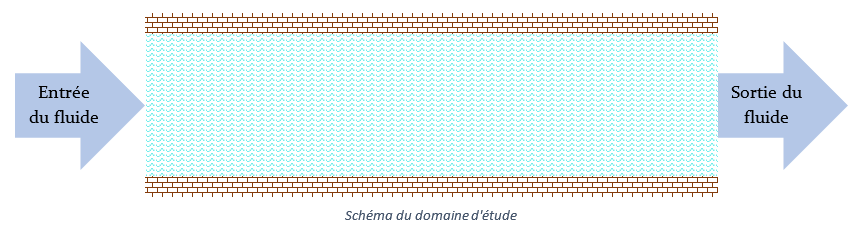
C’est dans ce domaine d’étude et selon des conditions d’expériences différentes que les simulations ont été réalisées.
On propose les expériences suivantes :
Experience 1
Cette expérience se réalise selon les conditions suivantes :
Viscosité non nulle
Différence de pression entre l'entrée et la sortie
Pas de temps constant (0.1s)
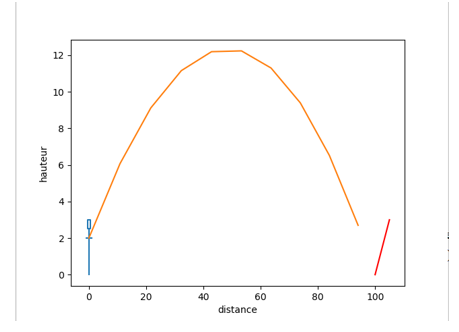
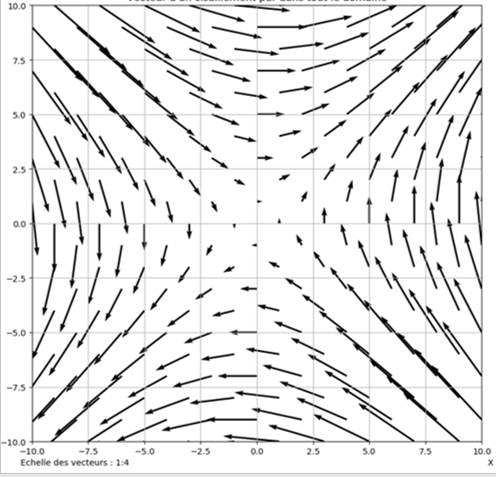
Cinquième itération en présence de gravité:
Quinzième itération sans présence de gravité:
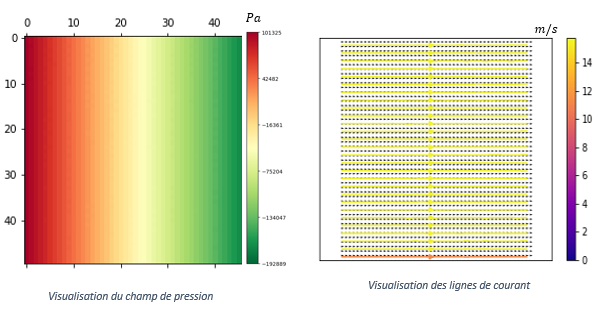
Experience 2
Cette expérience se réalise selon les conditions suivantes :
Viscosité non nulle
Vitesse horizontale imposée en entrée
Pas de composante verticale de la vitesse en entrée
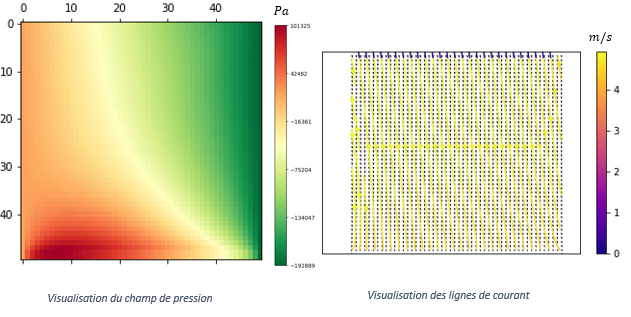
Gravité prise en compte
Quinzième itération :